Volumes of prisms and cylinders quick check delves into the captivating world of geometry, exploring the fascinating shapes of prisms and cylinders and their volumetric properties. This quick check provides a comprehensive overview of these shapes, their formulas, and their practical applications, offering a valuable resource for students and professionals alike.

Prisms and cylinders are fundamental geometric shapes with distinct characteristics. Prisms possess flat polygonal bases and parallel sides, while cylinders are characterized by their circular bases and curved surfaces. Understanding the volumes of these shapes is crucial for various fields, including engineering, architecture, and manufacturing.

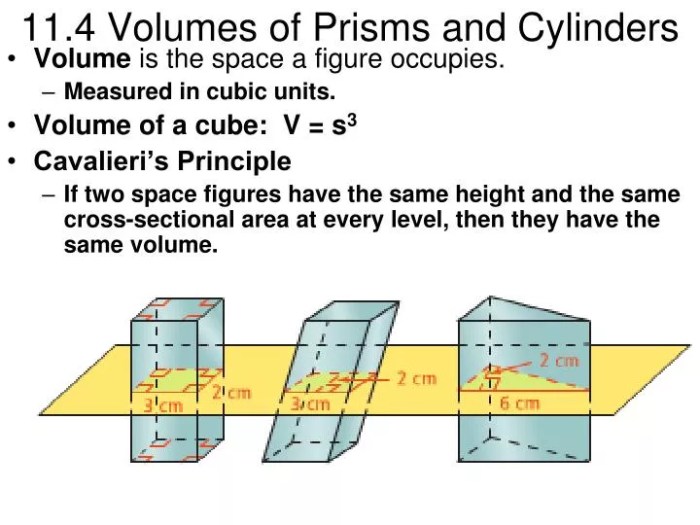
Volumes of Prisms and Cylinders

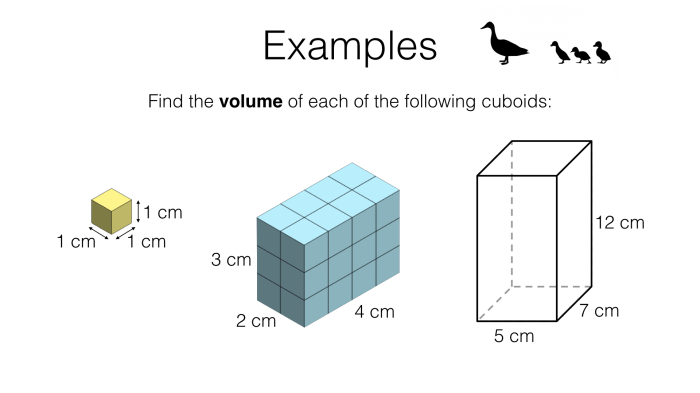
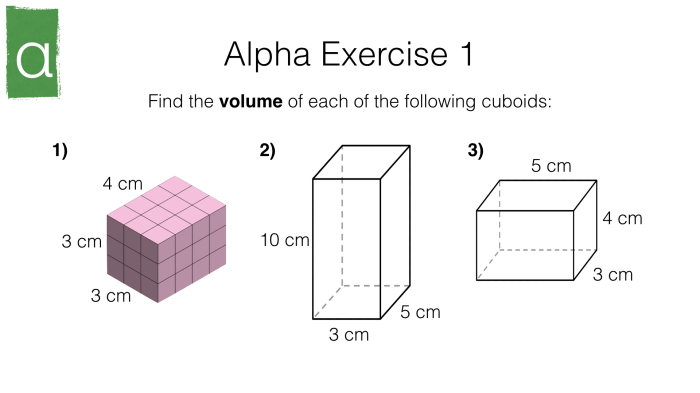
In geometry, the volume of a three-dimensional shape measures the amount of space it occupies. Two common three-dimensional shapes are prisms and cylinders. Understanding the formulas for calculating their volumes is crucial in various fields, including engineering, architecture, and manufacturing.

Definition of Prism, Volumes of prisms and cylinders quick check

A prism is a polyhedron with two parallel and congruent bases connected by rectangular faces. The bases can be any shape, but the most common prisms have triangular, square, or hexagonal bases.

The volume of a prism is calculated using the formula:

V = Bh

where V is the volume, B is the area of the base, and h is the height of the prism.

Examples of prisms in everyday life include boxes, pyramids, and triangular prisms.

Definition of Cylinder

A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. The height of a cylinder is the distance between the two bases.

The volume of a cylinder is calculated using the formula:

V = πr²h

where V is the volume, r is the radius of the base, and h is the height of the cylinder.

Examples of cylinders in everyday life include cans, pipes, and cylindrical tanks.

Comparing Volumes of Prisms and Cylinders

The formulas for calculating the volumes of prisms and cylinders share similarities and differences. Both formulas involve multiplying the area of the base by the height. However, the area of the base for a prism is typically a polygon, while the area of the base for a cylinder is a circle.

To determine which shape has a larger volume given specific dimensions, simply calculate the volume using the appropriate formula and compare the results.

Real-World Applications

Calculating the volumes of prisms and cylinders has practical applications in various fields:

• Engineering: Engineers use volume calculations to design structures, determine the capacity of tanks and containers, and analyze fluid flow.
• Architecture: Architects use volume calculations to determine the size of buildings, estimate construction costs, and design spaces that meet specific requirements.
• Manufacturing: Manufacturers use volume calculations to determine the amount of material needed for production, optimize packaging, and ensure product quality.

Understanding the volumes of prisms and cylinders is essential for solving real-world problems and making informed decisions in these fields.

FAQ Guide: Volumes Of Prisms And Cylinders Quick Check

What is the formula for calculating the volume of a prism?

Volume of prism = Base area × Height

How do I find the volume of a cylinder?

Volume of cylinder = π × Radius² × Height

What are some examples of prisms in everyday life?

Boxes, bricks, triangular prisms (rooftops)

What are some examples of cylinders in everyday life?

Cans, pipes, cylindrical tanks

Feature	Prism	Cylinder
Base shape	Polygon	Circle
Volume formula	V = Bh	V = πr²h