Express in scientific notation. 417.8 – Expressing numbers in scientific notation, like 417.8, is a powerful tool for representing very large or small numbers in a concise and manageable way. This notation simplifies complex calculations, making it widely used in scientific and engineering fields. In this article, we will explore the concept of scientific notation, its applications, and the steps involved in expressing numbers like 417.8 in this format.
Scientific notation is a method of expressing numbers as the product of a coefficient and a base raised to a power of ten. The coefficient is a number between 1 and 10, while the exponent represents the number of times the base is multiplied by itself.
For example, 417.8 can be expressed in scientific notation as 4.178 x 10 2.
Expressing in Scientific Notation: Express In Scientific Notation. 417.8

Scientific notation is a way of expressing very large or very small numbers in a more compact and manageable form. It is commonly used in scientific and engineering fields to represent values that would otherwise be difficult or cumbersome to write out in standard decimal notation.
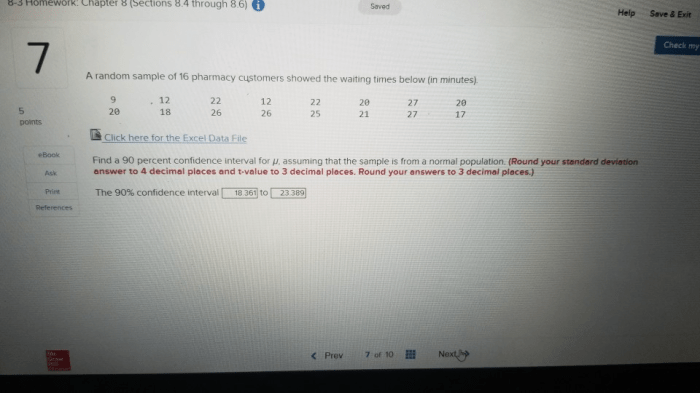
A number is expressed in scientific notation when it is written as a coefficient between 1 and 10, multiplied by a power of 10. The coefficient represents the significant digits of the number, while the exponent of 10 indicates the position of the decimal point.
Examples of Numbers Expressed in Scientific Notation
- 3.14 x 10 3= 3140
- 6.022 x 10 23= 602,200,000,000,000,000,000,000
- 2.998 x 10 8= 299,800,000
- 1.673 x 10 -24= 0.000000000000000000000000001673
- 5.23 x 10 -9= 0.00000000523
Steps Involved in Expressing a Number in Scientific Notation
- Move the decimal point to the left or right until there is only one non-zero digit to the left of the decimal point.
- Count the number of places the decimal point was moved.
- If the decimal point was moved to the left, the exponent of 10 will be positive. If the decimal point was moved to the right, the exponent of 10 will be negative.
- The exponent of 10 will be equal to the number of places the decimal point was moved.
- Write the number as a coefficient between 1 and 10, multiplied by 10 raised to the power of the exponent.
Analyzing 417.8
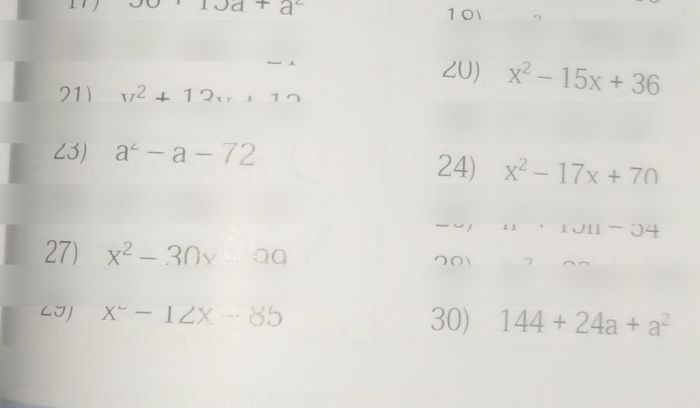
Scientific notation is a way of expressing very large or very small numbers in a more compact and convenient form. It is used in many scientific and engineering applications.
To convert a number to scientific notation, we move the decimal point until there is only one non-zero digit to the left of the decimal point. We then count the number of places we moved the decimal point and multiply the number by 10 raised to the power of the number of places we moved the decimal point.
Converting 417.8 to Scientific Notation
To convert 417.8 to scientific notation, we move the decimal point one place to the left, giving us 4.178. We then multiply this number by 10 raised to the power of 1, giving us 4.178 – 10^1.
Identifying the Coefficient and Exponent
The coefficient of a number in scientific notation is the number to the left of the – 10^n term. The exponent of a number in scientific notation is the number to the right of the – 10^n term.
In the case of 4.178 – 10^1, the coefficient is 4.178 and the exponent is 1.
Significance of the Exponent
The exponent in scientific notation indicates the order of magnitude of the number. A positive exponent indicates that the number is greater than 1, while a negative exponent indicates that the number is less than 1.
For example, the number 10^6 is 1 million, while the number 10^-6 is 0.000001.
Applications of Scientific Notation

Scientific notation, a powerful tool in mathematics and science, simplifies calculations involving very large or small numbers. It expresses numbers in the form of a × 10 n, where ‘a’ is a number between 1 and 10, and ‘n’ is an integer representing the number of times 10 is multiplied by itself.
This concise notation offers several practical applications across various fields:
Astronomy, Express in scientific notation. 417.8
- Expressing the vast distances between celestial bodies (e.g., 1.5 × 10 11kilometers from Earth to the Sun)
- Quantifying the immense size of stars (e.g., the radius of Betelgeuse is approximately 9.5 × 10 8kilometers)
Physics
- Describing subatomic particles and their properties (e.g., the mass of an electron is 9.11 × 10 -31kilograms)
- Expressing the speed of light (2.998 × 10 8meters per second)
Chemistry
- Representing the concentrations of substances in solutions (e.g., 0.0015 M = 1.5 × 10 -3M)
- Quantifying the size of molecules and atoms (e.g., the diameter of a carbon atom is 1.54 × 10 -10meters)
Medicine
- Expressing drug dosages (e.g., 100 milligrams = 1 × 10 -1grams)
- Quantifying blood cell counts (e.g., 5 × 10 9red blood cells per liter)
Engineering
- Describing the dimensions of large structures (e.g., the height of the Burj Khalifa is 8.28 × 10 2meters)
- Quantifying the force exerted by a machine (e.g., 2.5 × 10 3newtons)
By representing numbers in a concise and manageable form, scientific notation simplifies complex calculations, enhances understanding of scientific concepts, and facilitates effective communication of numerical data across various disciplines.
Comparisons and Conversions

Scientific notation is a compact way to represent very large or very small numbers. It is based on the idea of using a base number (usually 10) raised to a power. For example, the number 417.8 can be written in scientific notation as 4.178 x 10 2.Scientific
notation has several advantages over other number representation methods. First, it is more compact. For example, the number 417.8 written in decimal notation takes up four digits, while in scientific notation it takes up only three digits. Second, scientific notation makes it easier to compare very large or very small numbers.
For example, it is easier to compare the numbers 4.178 x 10 2and 6.34 x 10 3than it is to compare the numbers 417.8 and 6,340.However, scientific notation also has some disadvantages. First, it can be more difficult to read and write than decimal notation.
Second, it can be more difficult to perform arithmetic operations on numbers written in scientific notation.There are several methods for converting between scientific notation and other number formats. One method is to use the following formula:“`number in scientific notation = mantissa x 10 exponent“`where the mantissa is the number without the exponent, and the exponent is the power to which 10 is raised.For
example, to convert the number 4.178 x 10 2to decimal notation, we would use the following formula:“`
178 x 102= 4.178 x 100 = 417.8
“`Another method for converting between scientific notation and other number formats is to use a calculator. Most calculators have a button that can be used to convert numbers between scientific notation and decimal notation.
Converting Between Scientific Notation and Other Number Formats
There are several methods for converting between scientific notation and other number formats. One method is to use the following formula:“`number in scientific notation = mantissa x 10 exponent“`where the mantissa is the number without the exponent, and the exponent is the power to which 10 is raised.For
example, to convert the number 4.178 x 10 2to decimal notation, we would use the following formula:“`
178 x 102= 4.178 x 100 = 417.8
“`Another method for converting between scientific notation and other number formats is to use a calculator. Most calculators have a button that can be used to convert numbers between scientific notation and decimal notation.
Mathematical Operations in Scientific Notation

Performing mathematical operations on numbers expressed in scientific notation requires aligning the exponents of the factors involved. This ensures that the operations are carried out correctly and the resulting answer is expressed in the appropriate scientific notation form.
Addition and Subtraction
To add or subtract numbers in scientific notation, the exponents of the factors must be aligned. If the exponents are not the same, the factors should be rewritten so that they have the same exponent. Then, the coefficients can be added or subtracted, and the exponent remains the same.
For example, to add 2.34 x 10 3and 4.56 x 10 2, we first rewrite 4.56 x 10 2as 0.456 x 10 3to align the exponents. Then, we add the coefficients to get 2.34 x 10 3+ 0.456 x 10 3= 2.8 x 10 3.
Multiplication
To multiply numbers in scientific notation, the coefficients are multiplied, and the exponents are added. For example, to multiply 2.34 x 10 3by 4.56 x 10 2, we multiply the coefficients to get 2.34 x 4.56 = 10.6944, and then add the exponents to get 3 + 2 = 5. Therefore, the product is 10.6944 x 10 5.
Division
To divide numbers in scientific notation, the coefficient of the dividend is divided by the coefficient of the divisor, and the exponent of the divisor is subtracted from the exponent of the dividend. For example, to divide 2.34 x 10 3by 4.56 x 10 2, we divide the coefficients to get 2.34 / 4.56 = 0.513, and then subtract the exponents to get 3 – 2 = 1. Therefore, the quotient is 0.513 x 10 1.
FAQ Overview
What is the coefficient in the scientific notation of 417.8?
4.178
What is the exponent in the scientific notation of 417.8?
2
How do you convert 417.8 to scientific notation?
417.8 = 4.178 x 10 2
What are the advantages of using scientific notation?
Scientific notation simplifies calculations involving very large or small numbers and facilitates the comparison of quantities spanning several orders of magnitude.